Good question If you are using an equation for lgebra/quadratics/transformingquadraticfunctions/v/shiftingandscalingparabolasThe vertex of parabola x 2 4y 3x = 2 is 32 1716 32 116 0 0 0 32 Rewrite the given equation as followsx 2 3x = 4y 2x 2 3x 94 = 4y 20) This is the parent function, in red 1) The function has been shifted to the right by one unit (in blue) 2) The funct

The Line Y X 2 Cuts The Parabola Y 2 8x In The Points A And B The Normals Drawn To Youtube
Y=(x-h)^2+k parabola
Y=(x-h)^2+k parabola-The transformations are all illustrated in the graph below Note especially the order in which they occur This is important!A line L y = m x 3 meets yaxis at E (0, 3) and the arc of the parabola y 2 = 1 6 x, 0 ≤ y ≤ 6 at the point F (x 0 , y 0 ) The tangent to the parabola at F (x 0 , y 0 ) intersects the yaxis at G (0, y 1 ) The slope m of the line L is chosen such that the area of the E F G has a local maximum Match List 1 with List 2




Quadratic Function
Algebra Graph y=xx^2 y = x − x2 y = x x 2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Reorder x x and − x 2 x 2 y = − x 2 x y = x 2 xThe "general" form of a parabola's equation is the one you're used to, y = ax 2 bx c — unless the quadratic is "sideways", in which case the equation will look something like x = ay 2 by c The important difference in the two equations is in which variable is squared for regular (vertical) parabolas, the x part is squared;17 hours ago I had this question and saw the other thread, and the proof of why all quadratics were parabolas started with the axiom that y = x 2 is a parabola well I don't really understand why y = x 2 is a parabola I get that if you plot it you get a parabola, but why is that the case?
y = x 2, where x ≠ 0 Here are a few quadratic functions y = x 2 5; 2 Rotating the parabola y = x2 by θ clockwise gives v = u2, where (u v) = (cosθ − sinθ sinθ cosθ)(x y) ie xsinθ ycosθ = (xcosθ − ysinθ)2 Putting θ = π 4 gives 1 √2(x y) = ( 1 √2(x − y))2√2(x y) = (x − y)2 which when expanded is x2 y2 − 2xy − √2x − √2y = 0 Share edited Jul 19 '17 at 1606Graphing y = (x h)2 k In the graph of y = x2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y
Answer to Consider F and C below F(x, y) = x^2 i y^2 j, C is the arc of the parabola y = 2x^2 from (2, 8) to (2, 8) (a) Find a function fGraph the parabola, y =x^21 by finding the turning point and using a table to find values for x and yParabola The standard form equation of a general quadratic (polynomial functions of degree 2) function is f(x) = ax 2 bx c where a ≠ 0 If b = 0, the quadratic function has the form f(x) = ax 2 c Since f(x) = a(x) 2 c = ax 2 c = f(x), Such quadratic functions are even functions, which means that the yaxis is a line of symmetry of the graph of f
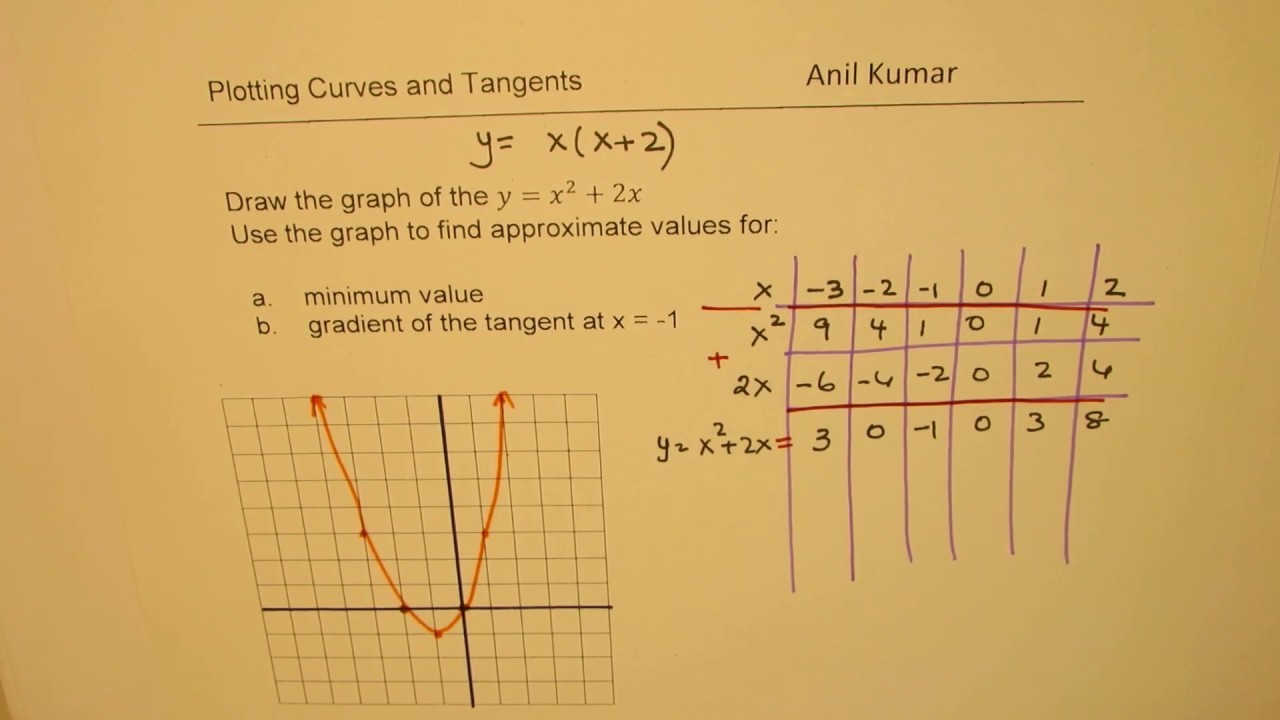



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




The Line Y X 2 Cuts The Parabola Y 2 8x In The Points A And B The Normals Drawn To Youtube
Yes, its axis of symmetry is the xaxis If you have a quadratic equation in two unknowns, mathAx^2BxyCy^2DxEyF=0/math you can tell if the curve it represents is a parabola or not by its discriminant mathB^24AC/math If tStep 1 Solve for the vertex of the parabola The vertex of a parabola of the form {eq}y= x^2 bx c {/eq} is always given by {eq}\left (\dfrac {b} {2a},f (\dfrac {b} {2a})\right) {/eq} StepA parabola is a symmetrical, curved, Ushaped graph The equation of a parabola graph is y = x² Parabolas exist in everyday situations, such as the path of an object in the air, headlight shapes



Solution Graph Y X 2 1 Label The Vertex And The Axis Of Symmetry And Tell Whether The Parabola Opens Upward Or Downward
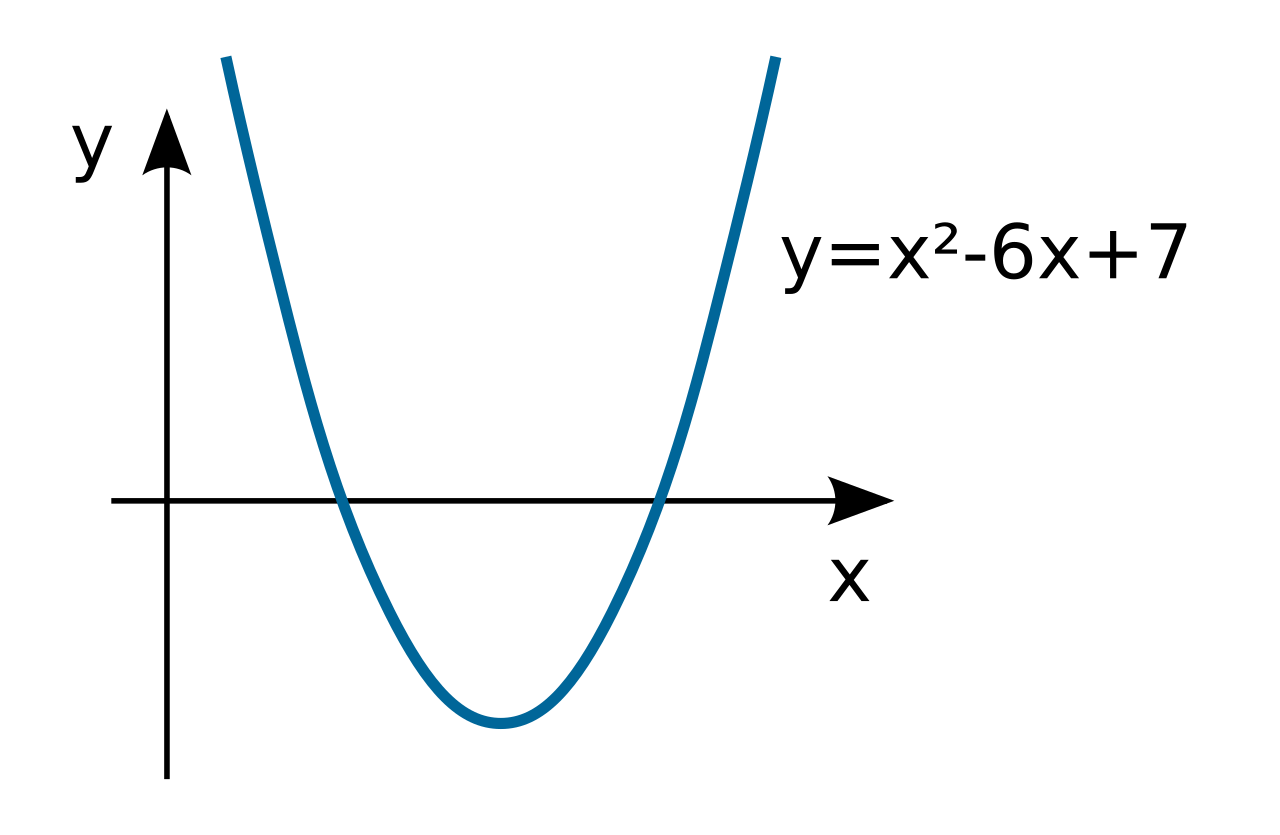



File Parabola Y X 6x 7 Svg Wikimedia Commons
Two points with abscissas x 1 = 1 a n d x 2 = 3 taken on the parabola of the y = x 2 A secant is drawn to it is parallel to the secant Write the equation of the secant and the tangentThe graph of the quadratic function is a Ushaped curve is called a parabola The graph of the equation y = x2, shown below, is a parabola (Note that this is a quadratic function in standard form with a = 1 and b = c = 0) In the graph, the highest or lowest point of a parabola is the vertex The coordinates of a point on the parabola y =x 2 7x 2 which is closet to the straight line y = 3x – 3 is (A) (–2, 8) (B) (–2, –8) (2, –8) (D) (2, ) jee;




Quadratic Systems A Line And A Parabola Video Khan Academy
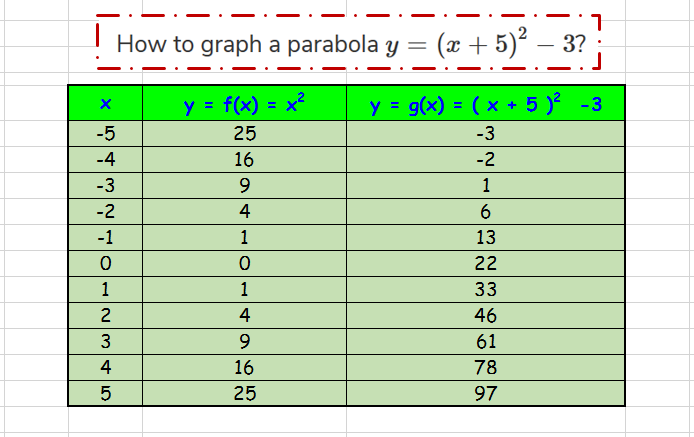



How To Graph A Parabola Y X 5 2 3 Socratic
A Quadratic Equation takes the form y = ax2 bx c Graph of a quadratic function forms a Parabola The coefficient of the x2 term (a) makes the parabola wider or narrow If the coefficient of the x2, term (a) is negative then the parabola opens downPolynomials quadratics conicsections Share edited 1 min ago GaryY = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down Find the vertex ( h, k) ( h, k)




Graphing Parabolas



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com
Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downSal rewrites the equation y=5x^2x15 in vertex form (by completing the square) in order to identify the vertex of the corresponding parabola the easiest there's a formula for it and we talk about where that comes from in multiple videos where the vertex of a parabola or the x coordinate of the vertex of the parabola so the xcoordinateThe equation of the parabola comes out to be y2= 4px where the directrix is the verical line x=p and the focus is at (p,0) parabola "opens to the right" and if p 0 the parabola "opens to the left" The equations we have just established are known as the standard




Quadratic Function



What Is The Maximum Vertical Distance Between The Line Math Y X 2 Math And The Parabola Math Y X 2 Math For Math 1 Le X Le 2 Math Quora
Y = x 2 3x 13; Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the y intercept y = 12 x 2 48 x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for y y = 12 (0) 2 48 (0) 49 (Replace x with 0)Find the vertex, focus, directrix, latus rectum of the following parabola y 2 8y x 19 = 0 Solution Write the equation of parabola in standard form y 2 8y = x 19 y 2 2(y)(4) 4 2 4 2 = x 19 (y 4) 2 4 2 = x 19 (y 4) 2 16 = x 19 Add 16 to each side (y 4) 2 = (x 3)



Graphing Quadratic Functions



Quadratics Graphing Parabolas Sparknotes
(2, 4) The easiest way is y=ax^2bx c axis on symmetry is aos = (b)/(2a) Vertex is (aos, f(aos)) c = yintercept so your function y = x^2 4x a = 1 b = 4 c = 0 aos = ((4))/(2*1) = 2 f(aos) means we put the aos back in your function as x and solve for y f(aos) = f(2) = 2^2 4*2 = 4 Vertex is (aos, f(aos)) Vertex is (2, 4) Note, this can also be solved by completing the square and converting the function to vertex form graph{y = x^2 4x 713, 1287, 78, 22}The axis of symmetry will have the equation y = k Its form will be x = a( y – k) 2 h Example 1 Draw the graph of y = x 2 State which direction the parabola opens and determine its vertex, focus, directrix, and axis of symmetry The equation y = x 2 can be written as y = 1( x – 0) 2 0 so a = 1, h = 0, and k = 0The area bounded by the curve y 2 (2a x) = x 3 and the line x = 2a is The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x = 3π/2 is The area bounded by the curves y 2 = 8x and x 2 = 8y is The area bounded by y = sin1 x, x = 1 / √2 and xaxis is The area enclosed between the curve y = 1 x 2, the y
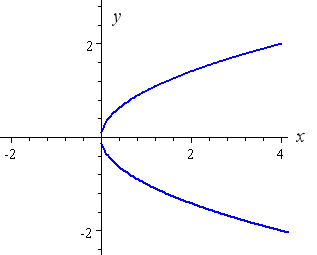



How To Draw Y 2 X 2 Interactive Mathematics




Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
What is the following parabola's axis of symmetry of $$ y =x^2 2x 3 $$ Answer Since this equation is in standard form, use the formula for standard form equation $$ x = \frac{ b}{ 2a} $$ Answer the axis of symmetry is the line $$ x = 1 $$ Problem 7 What is the following parabolaExploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the thirdWe're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0 Let's vary the value of a to determine how the graph changes
/asGF.jpg)



Axis Of Symmetry Parabola




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com
To find the endpoints, substitute x = 6 x = 6 into the original equation ( 6, ± 12) ( 6, ± 12) Next we plot the focus, directrix, and focal diameter, and draw a smooth curve to form the parabola Try It Graph y2 =−16x y 2 = − 16 x Identify and label the focus, directrix, and endpoints ofThe children are transformations of the parent Some functions will shift upward or downward, open wider or more narrow, boldly rotate 180 degrees, or a combination of the above Learn why a parabola opens wider, opens more narrow, or y = x ^ 26x 8 y = 0 we will solve it and find the intersection points of the parabola and the line x squared – 6 * x 8 = 0 Find the discriminant of the quadratic equation D = b squared – 4ac = (6) squared – 4 1 8 = 36 – 32 = 4 Since the discriminant is greater than zero, the quadratic equation has two real roots




How To Draw Y 2 X 2 Interactive Mathematics



Quadratics Graphing Parabolas Sparknotes
When graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if aShare It On Facebook Twitter Email 1 Answer 1 vote answered byGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Math Spoken Here Classes Quadratic Equations 3



Practice Exam 1
Key Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;Calculate parabola directrix given equation stepbystep \square!Foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2} en Related Symbolab blog posts My Notebook, the Symbolab way
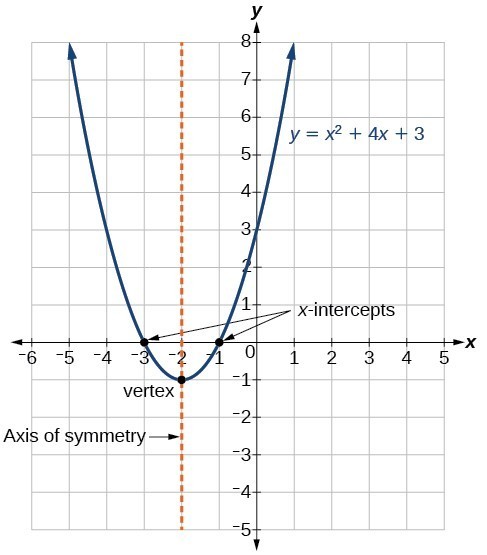



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra



Y X 2
Since the given equation involves x 2 {{x}^{2}} x 2, the axis of the parabola is the yaxis Equation of directrix, y = a ie = 4 Length of latus rectum = 4a = 16 Illustration 6 If the parabola y 2 = 4x and x 2 = 32y intersect at (16, 8) at an angle θ, then find the value of θ Solution The slope of the tangent to y 2 = 4x at (16, 8) isY = x 2 5x 3;The two parabolas y 2 = 4ax and x 2 = 4ay intersect The two parabolas y 2 = 4ax and x 2 = 4ay intersect A at two point on the line y = x B only at the origin C At three points one of which lies on y x = 0 D only at (4a, 4a) Please scroll down to see the correct answer and solution guide



Http Www Buckeyevalley K12 Oh Us Userfiles 74 Classes 17 2 1 2 notes Pdf



Assignment 2
The x coordinate of the vertex is the equation of the axis of symmetry of the parabola The vertex of the parabola is (2, 1) So, the axis of symmetry is the line x = 2 Find the axis of symmetry of the graph of y = x2 − 6x 5 using the formula For a quadratic function in standard form, y = ax2 bx c , the axis of symmetry is a The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetry The original question from Anuja asked how to draw y 2 = x − 4 In this case, we don't have a simple y with an x 2 term like all of the above examples Now we have a situation where the parabola is rotated Let's go through the steps, starting with a basic rotated parabola Example 6 y 2 = x The curve y 2 = x represents a parabola rotated




Find The Point On The Parabola 2y X 2 That Is Closest To The Point 4 1 Mathematics Stack Exchange




Scaling Reflecting Parabolas Video Khan Academy
If a parabola and a straight line intersect, that is, they have one or two common points, then at these points the values of y will coincide Therefore, we equate the righthand sides of the formulas of these functions If the resulting equation has a solution, then the line and the parabola intersect x² = 12 – x x² x – 12 = 0The given equation of the line is {eq}y = x 2 {/eq} and the parabola {eq}y = {x^2} {/eq} for {eq} 1 \le x \le 2 {/eq} The objective is to find the maximum vertical distance between the line I don't have a cluehow to fin the focus of a parabola Can somebody work through my sample question, so I can take a look and figure it out The question is Find the focus of the parabola y²=12x Thanks




Solution For The Parabola Y X 2 36 Graph Of A Parabola Opening Down At The Vertex 0 36 Crossing The X Axis At 6 0 And 6 0
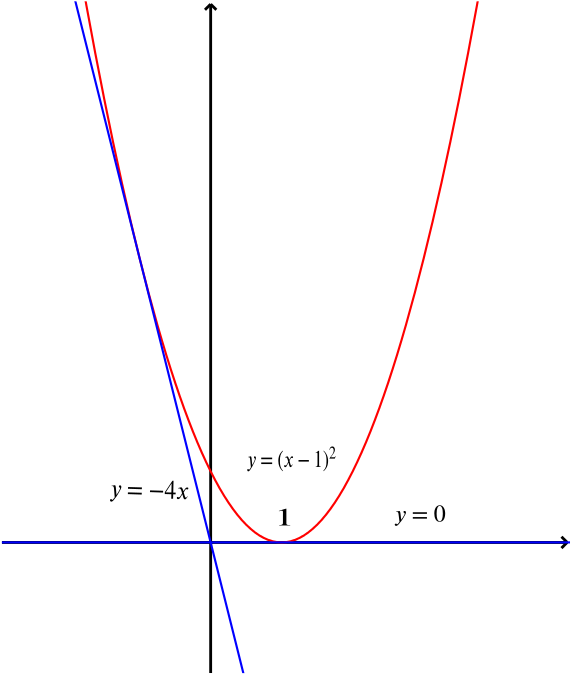



Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics




Consider The Parabola Y X 2 The Shaded Area Is Brainly In




Quadratic Function
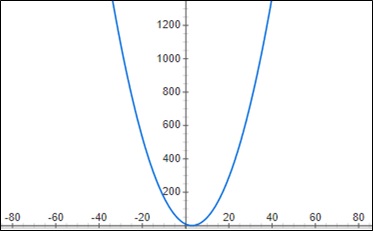



Sketch The Parabola Of Equation Y X 2 6x 9 And Indicate Its Vertex Study Com
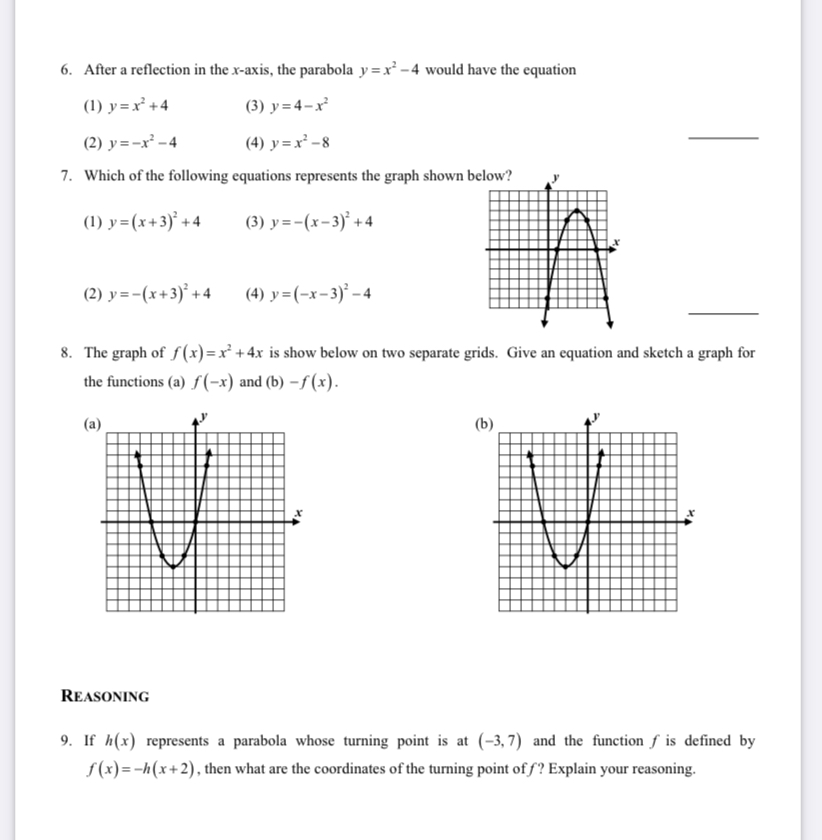



Answered 6 After A Reflection In The X Axis Bartleby



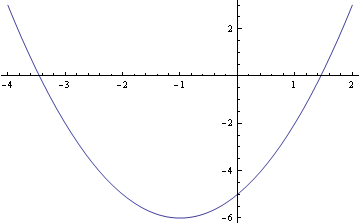
Ex 8 1 9 Class 12 Find Area Bounded By Parabola Y X 2 And Y X



Graphing Quadratic Functions




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram



Y X 2 8x 16 Mathskey Com



Where Is The Vertex Of The Parabola Y X2 2x 5 Blurtit




How To Sketch A Parabola Example 3 Y X 2 6x 10 College Cram Com




Consider The Parabola Whose Equation Is Y X 2 4x And The Line Y 2x B Then Whichfollowing Is Are Correct



Parabolas



Draw The Graph Of Y X 2 3x 2 And Use It To Solve X 2 2x 1 0 Sarthaks Econnect Largest Online Education Community



Quadratics Graphing Parabolas Sparknotes



A Parabola Symmetrical To Y X Line




Analyzing The Parabola Ppt Download




Graph Y X 2 Study Com




Graph Y X 2 3 Youtube




How To Graph A Parabola 13 Steps With Pictures Wikihow
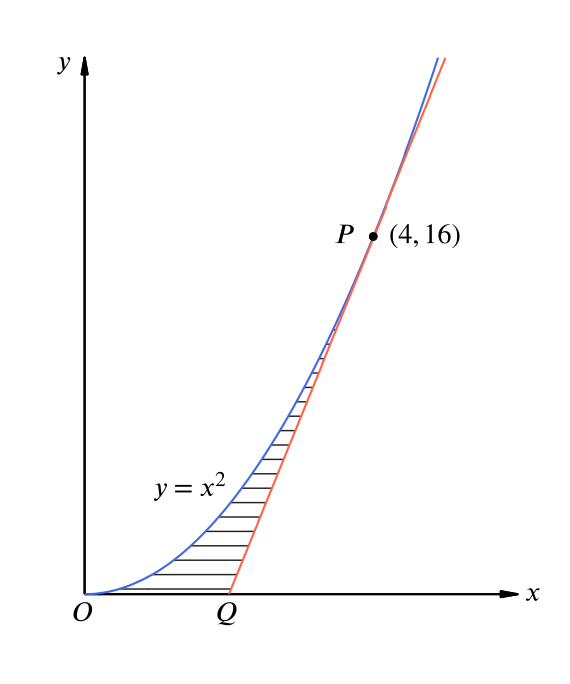



Solution Can We Find The Area Inside A Parabola A Tangent And The X Axis Calculus Of Powers Underground Mathematics
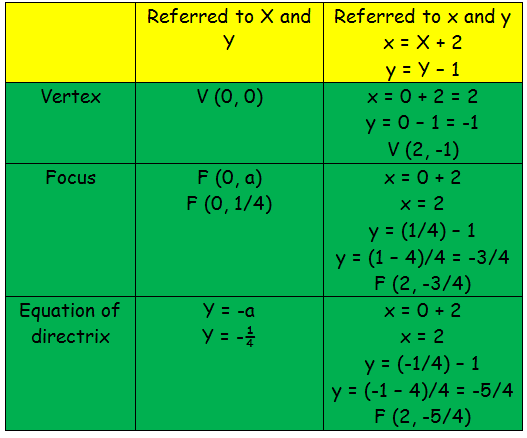



How To Find Focus Directrix And Vertex Of Parabola




Quadratic Function
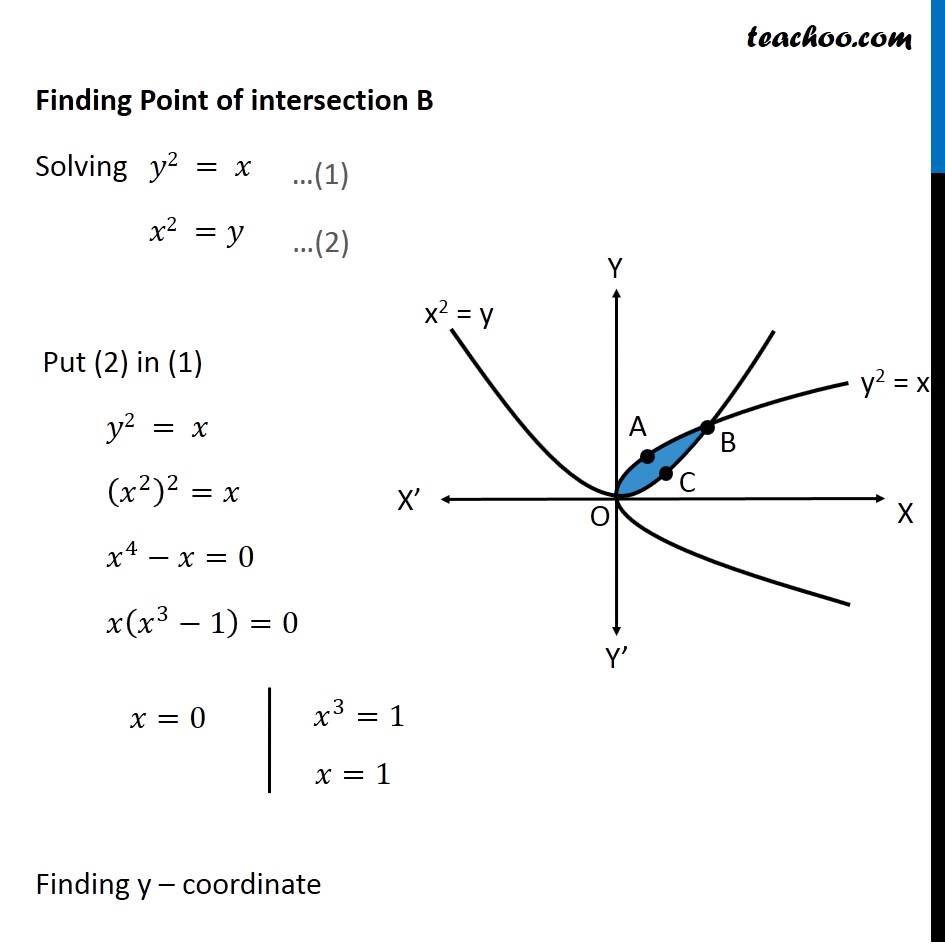



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X



Y X 2 12x 35 Math Homework Answers
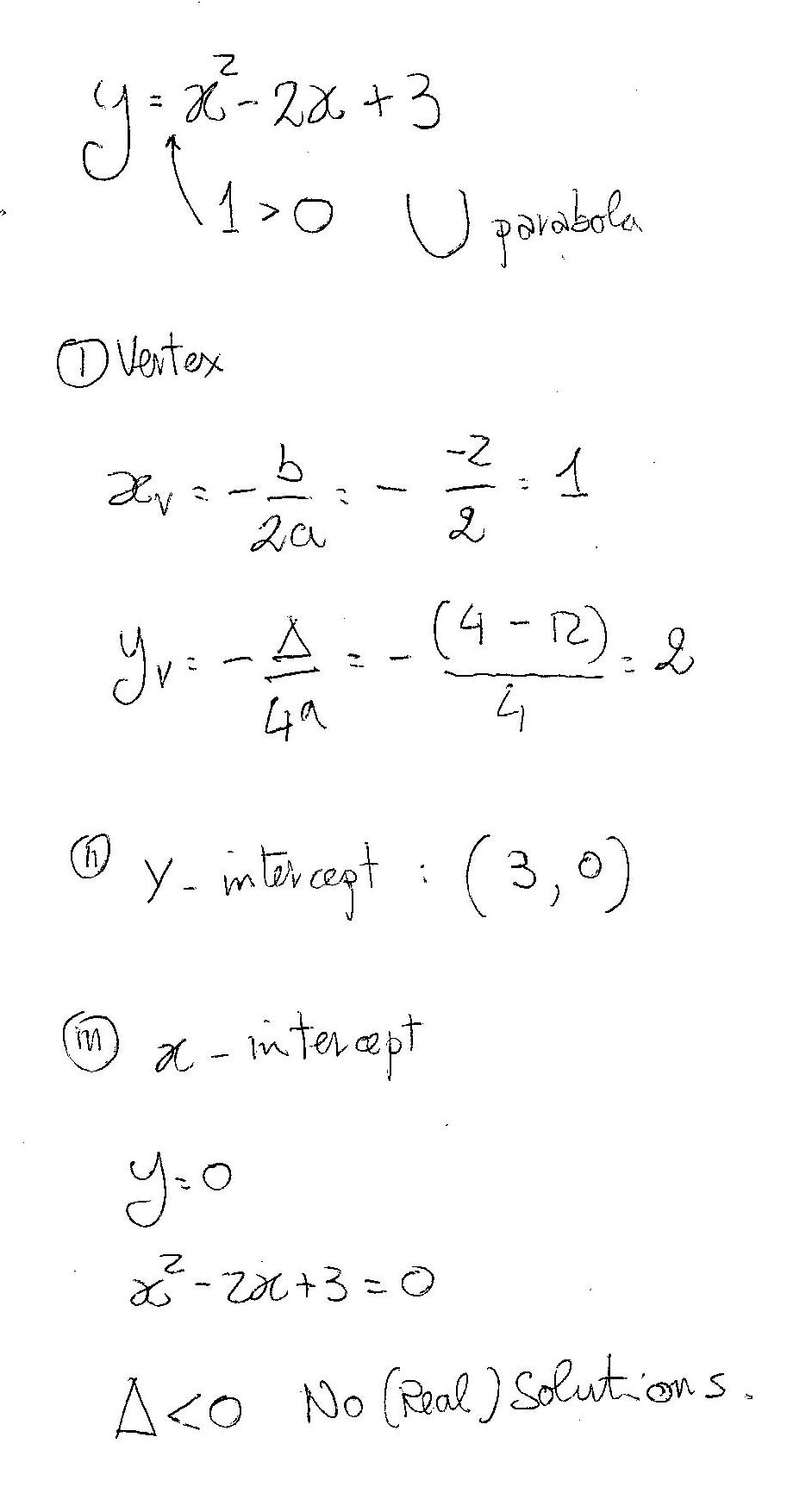



How Do You Graph Y X 2 2x 3 Socratic



Content Transformations Of The Parabola
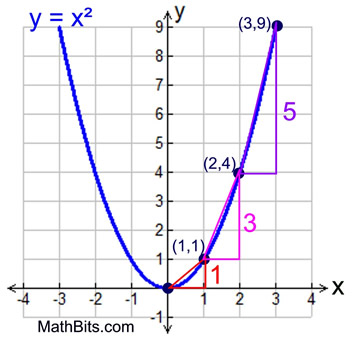



Quadratic Function Rate Of Change Mathbitsnotebook A1 Ccss Math




The Graph Of The Quadratic Function Y X2 Is Shown Below If This Parabola Is Reflected About The Brainly Com




Find The Coordinates Of A Point Of A Parabola Y X 2 7x 2 Which Is Closest To The Straig Youtube
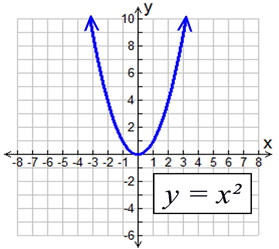



Parabola Parent Function Mathbitsnotebook A1 Ccss Math
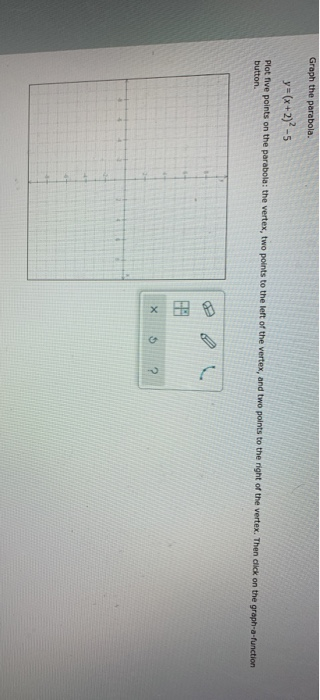



Graph The Parabola Y X 2 2 5 Plot Five Points On Chegg Com




How To Graph A Parabola 13 Steps With Pictures Wikihow



Quadratics Graphing Parabolas Sparknotes



Solution I Do Not Know How To Graph The Parabola Y X 2



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram




Parabola Complete



1



How Do You Graph The Parabola Y X 2 2 2 Using Vertex Intercepts And Additional Points Socratic




Parabola Parent Function Mathbitsnotebook A1 Ccss Math



How To Graph A Parabola Of Y X 1 X 5 Mathskey Com
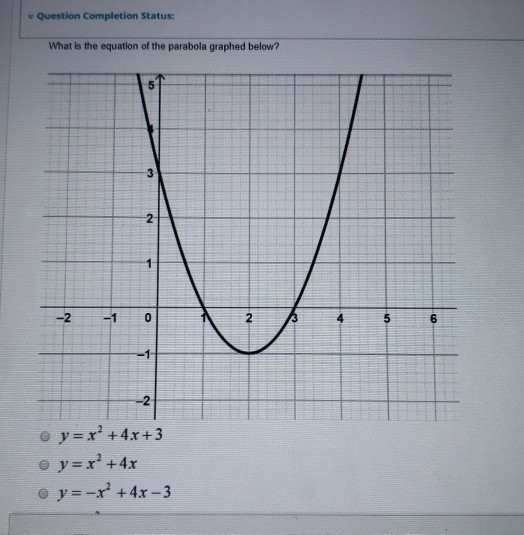



Question Completion Status What Is The Equation Of Chegg Com



Graph Of A Parabola Topics In Precalculus



Search Q Y 3d1 X Tbm Isch




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic



How To Draw A Sketch Of The Graph Of The Parabola Y X 2 8x 10 Quora
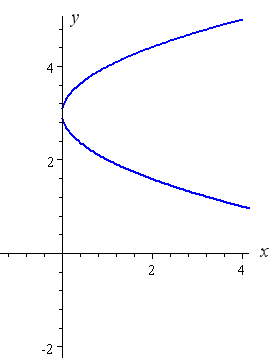



How To Draw Y 2 X 2 Interactive Mathematics



Graphing Quadratic Functions



Quadratic Function Parabola
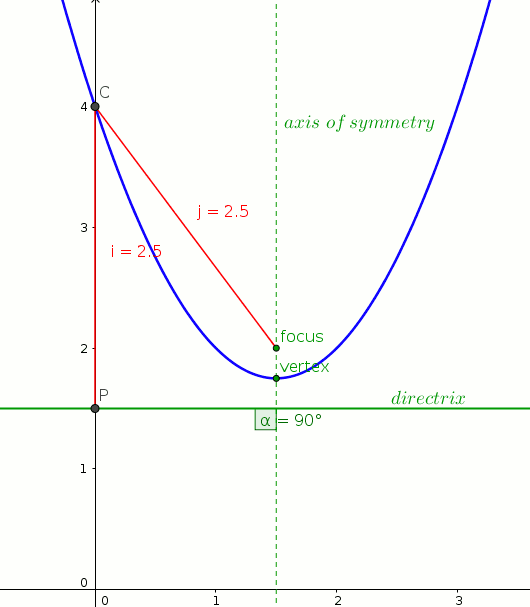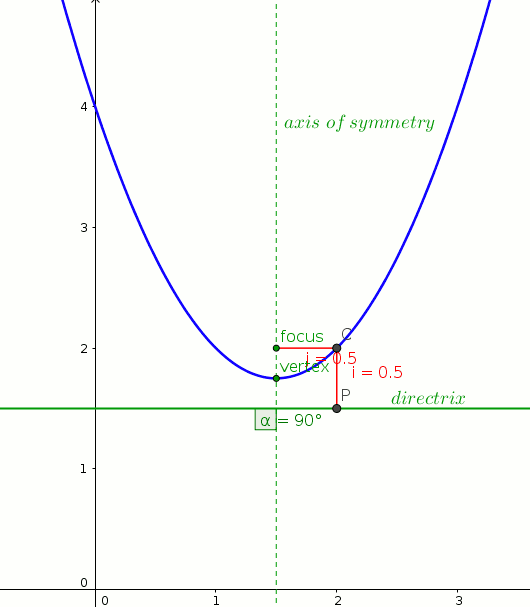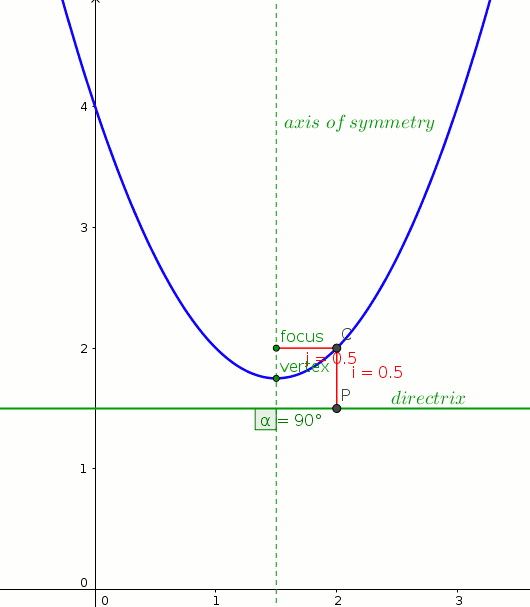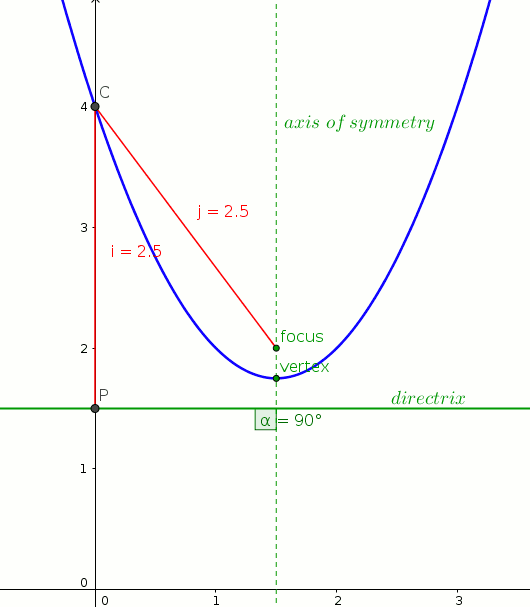



What Are The Vertex Focus And Directrix Of Y X 2 3x 4 Socratic




Example 15 Find Area X Y 0 Y X2 1 0 Y X 1



Content Transformations Of The Parabola




The Distance Between The Vertex Of The Parabola Y X 2 4x 3 And The Centre Of The Circle X 2 9 Y 3 2 Is
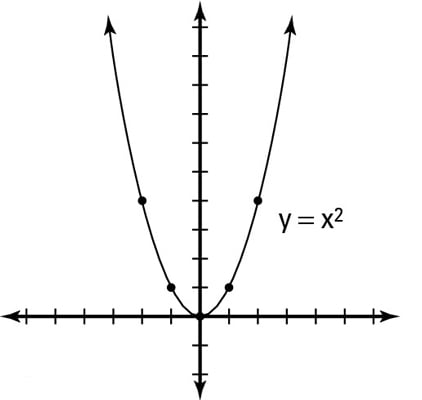



How To Graph A Vertical Parabola Dummies



Exploration Of Parabolas
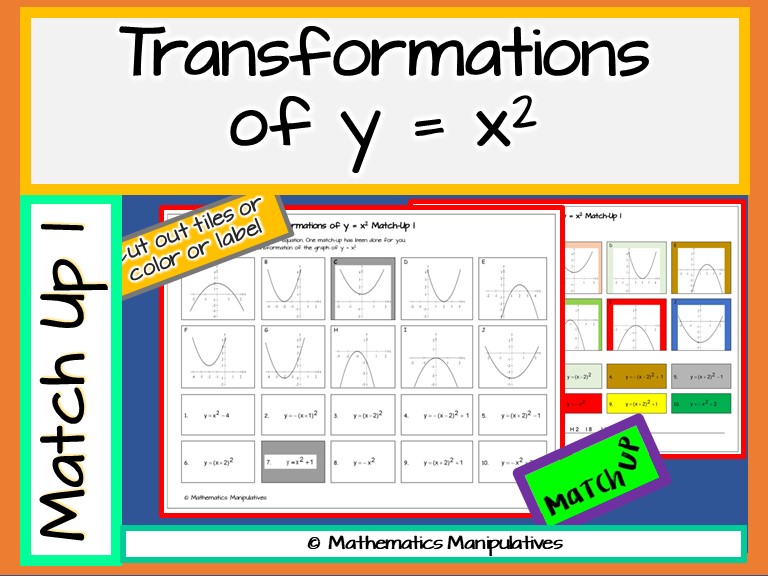



Algebra Parabola Transformations Of Y X 2 Graphs Match Up 1 Teaching Resources



Content Transformations Of The Parabola



Solution How To Graph A Parabola Using Y X2 2x 8
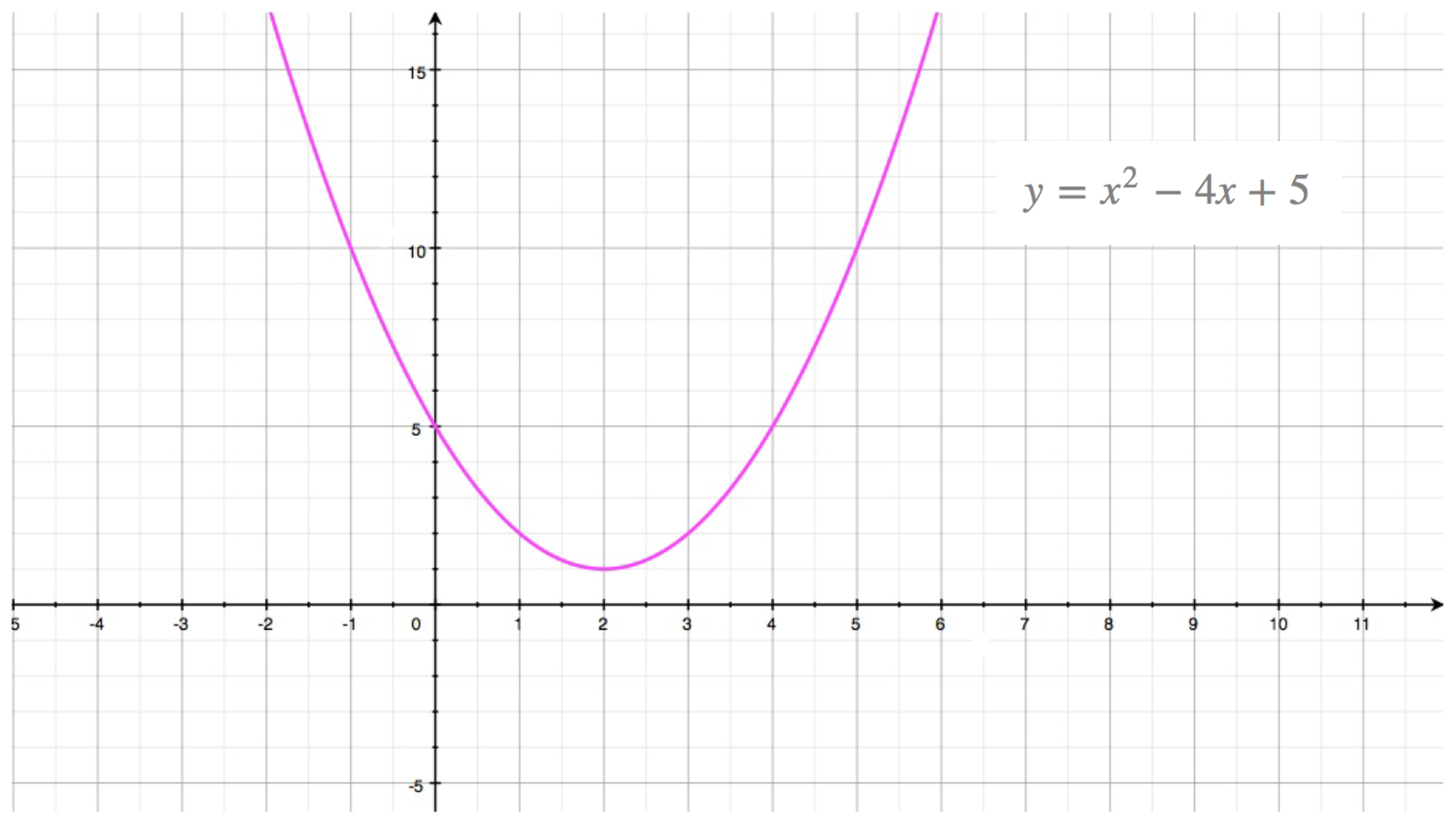



Quadratic Function Parabola



Graph The Parabola Y X 2 6x Mathskey Com
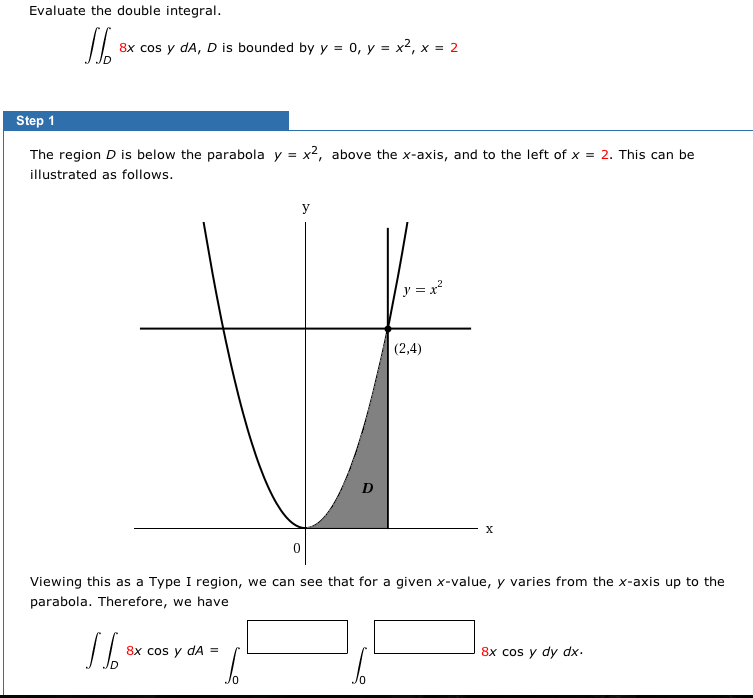



Evaluate The Double Integral The Region D Is Below Chegg Com



Solved 1 Compare The Graph Of Y X 2 To The Graph Of Y 0 6 X 2 A Which Graph Will Be Narrower Why B What Is The Position Of The Vertex For Eac Course Hero




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube
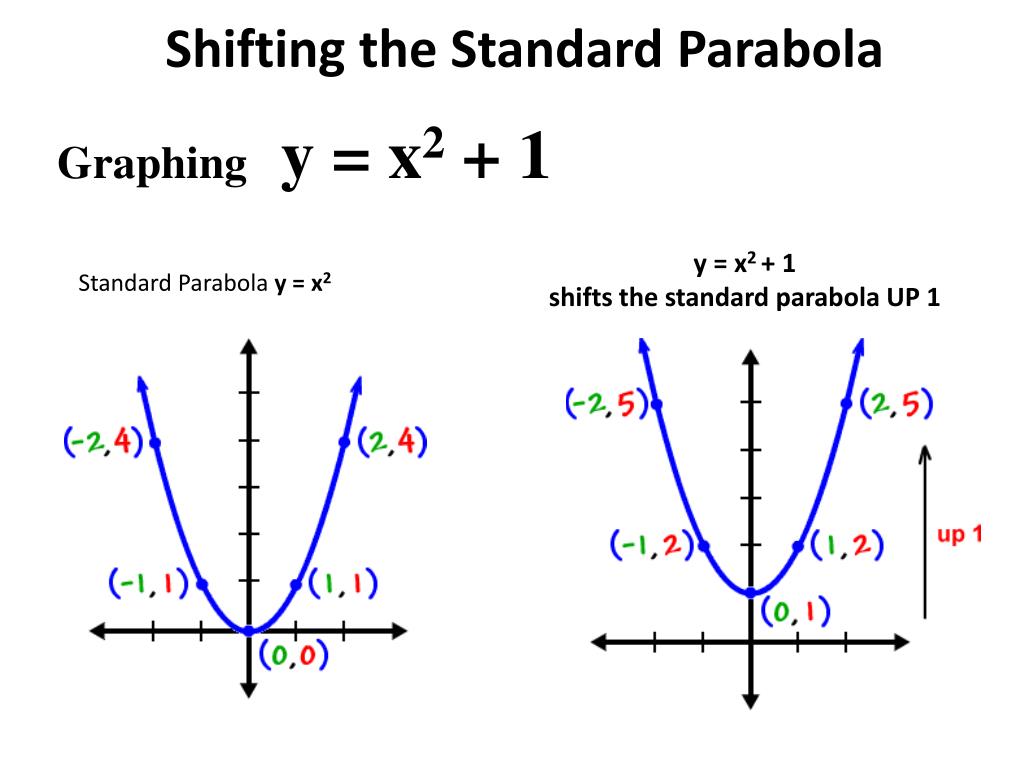



Ppt Shifting The Standard Parabola Powerpoint Presentation Free Download Id
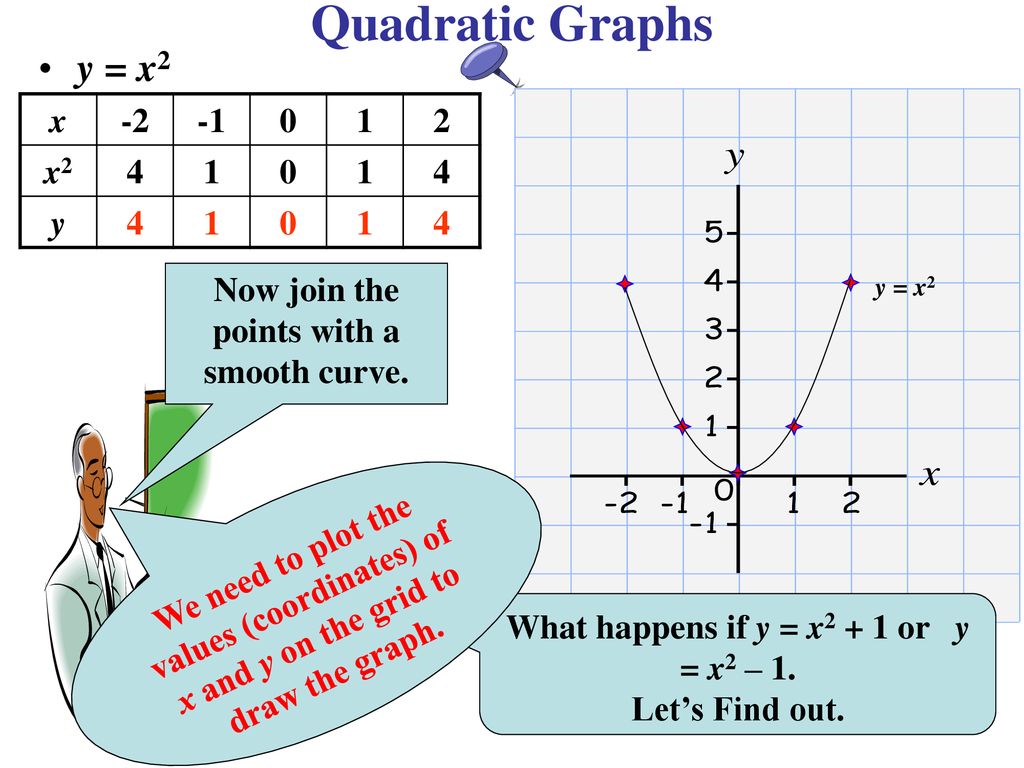



Quadratic Graphs Parabolas Ppt Download




Find The Area Of The Region Bounded By The Parabola Y X 2 And The Line Y 4 Study Com
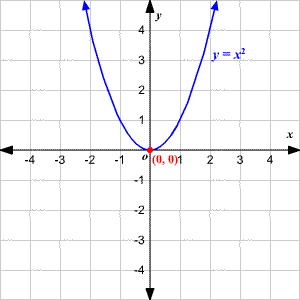



Parabolas
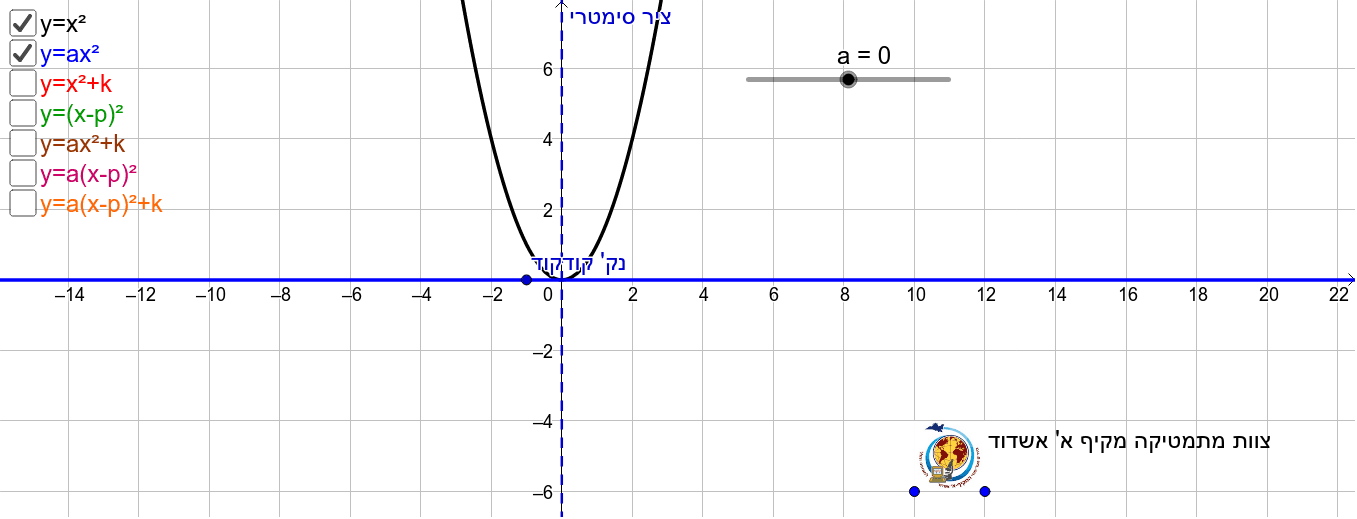



Parabola Y X 2 Geogebra



What Is The Point Of Intersection Of A Parabola Y X 2 2 And The Points 2 6 And 2 6 Quora
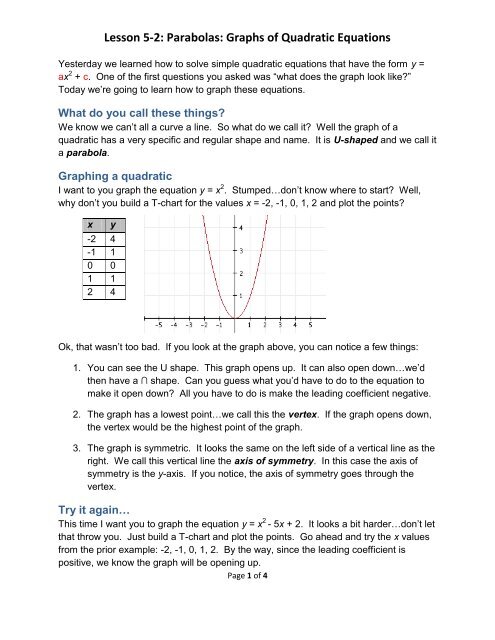



Lesson 5 2 Parabolas Graphs Of Quadratic Equations




Graphing Parabolas
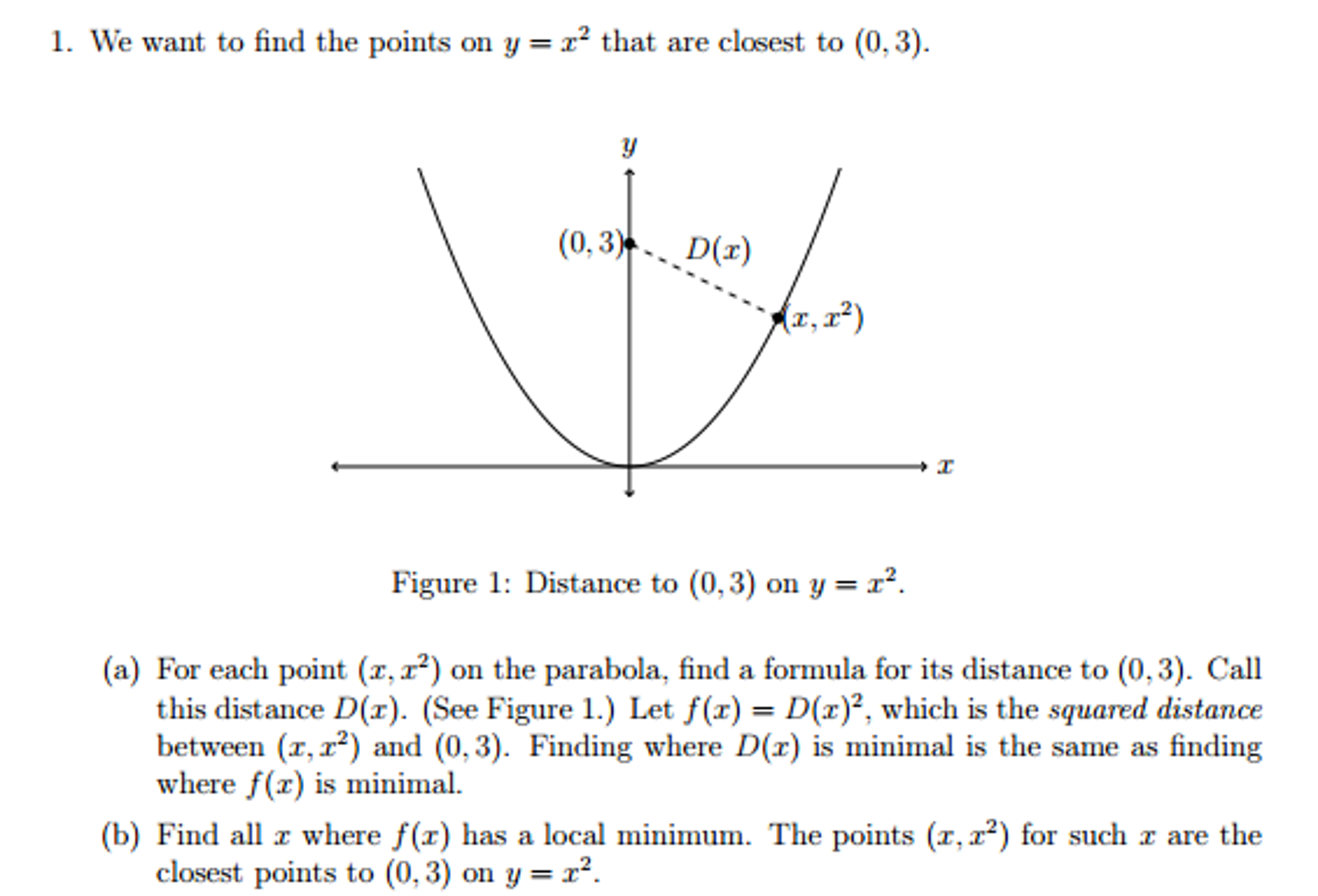



We Want To Find The Points On Y X 2 That Are Chegg Com




Find The Coordinates Of A Point On The Parabola Y X 2 7x 2 Which Is Closest To The Straight Line Y 3x 3



1




How To Draw Y 2 X 2 Interactive Mathematics



Exploration Of Parabolas


