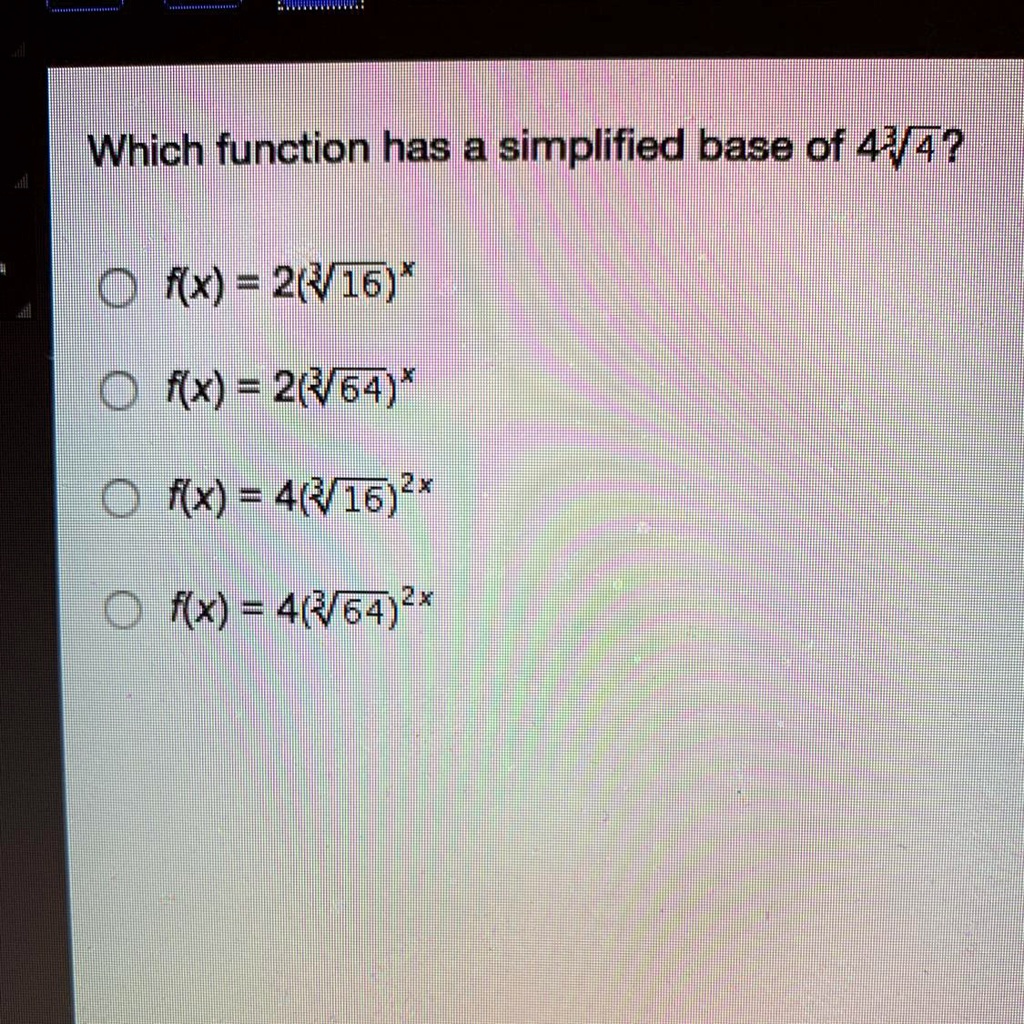
Browse Questions For Algebra
WebThe easiest way is to rewrite it as y= (x − 21)2 How do you find the zeros, real and imaginary, of y = x2 − x 7 using the quadratic formula?WebSystem of Equations Substitution Calculator Solve system of equations unsing substitution method stepbystep full pad » Examples Related Symbolab blog posts High School Math
The substitution method math
The substitution method math-WebStepbyStep Examples Algebra Solve by Substitution Calculator Step 1 Enter the system of equations you want to solve for by substitution The solve by substitution calculatorWebThe steps to apply or use the substitution method to solve a system of equations are given below Step 1 Simplify the given equation by expanding the parenthesis if needed Step 2

Ultralow Lattice Thermal Conductivity And Improved Thermoelectric Performance In Cl Doped Bi2te3 Xsex Alloys Acs Applied Materials Interfaces
Web x/2 y=081 7/x y/2=102 Multiply eqn2 with 2 Then you get it as 14/xy= Now you subtract eqn1 from 2 14x^2/2x=92now you equate the value of xWebHow to Use the Calculator Type your algebra problem into the text box For example, enter 3x2=14 into the text box to get a stepbystep explanation of how to solve 3x2=14 TryWebIn the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3 Using the
WebAlgebra Solve by Substitution xy=8 , xy=2 x y = 8 x y = 8 , x − y = 2 x y = 2 Subtract y y from both sides of the equation x = 8− y x = 8 y x−y = 2 x y = 2 Replace all7/ (x y 2 y 2) = 10 pair of linear equations in two variables class10 1 Answer 0 votes answeredWebSubstitution Method Calculator This method involves first solving for one of the variables with one equation and then substituting the results in the second equation Our algebra
The substitution method mathのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
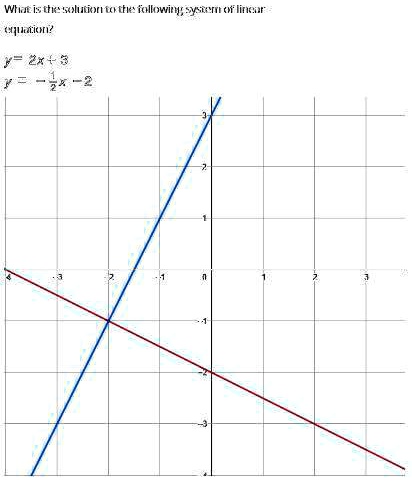 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind | 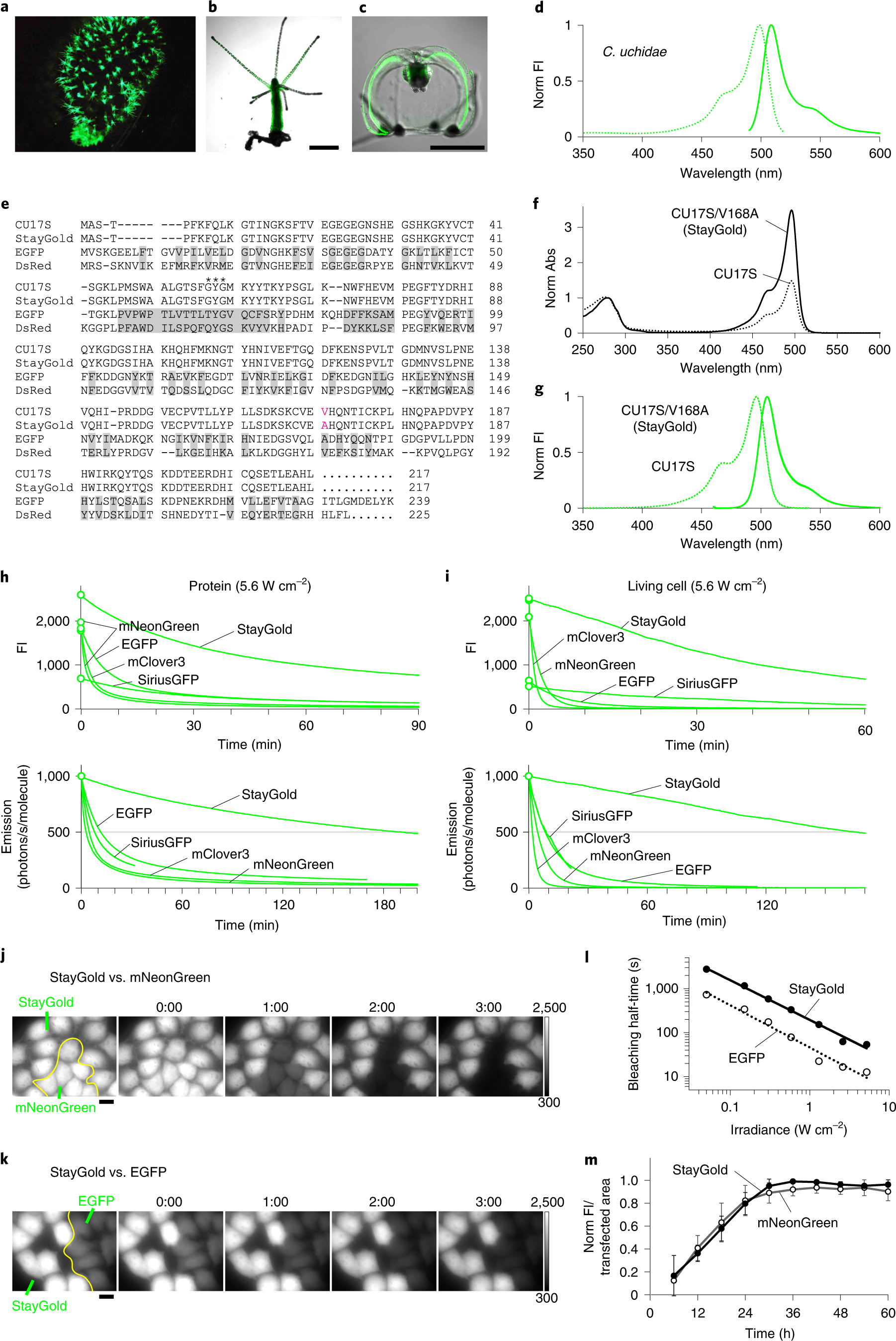 Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | 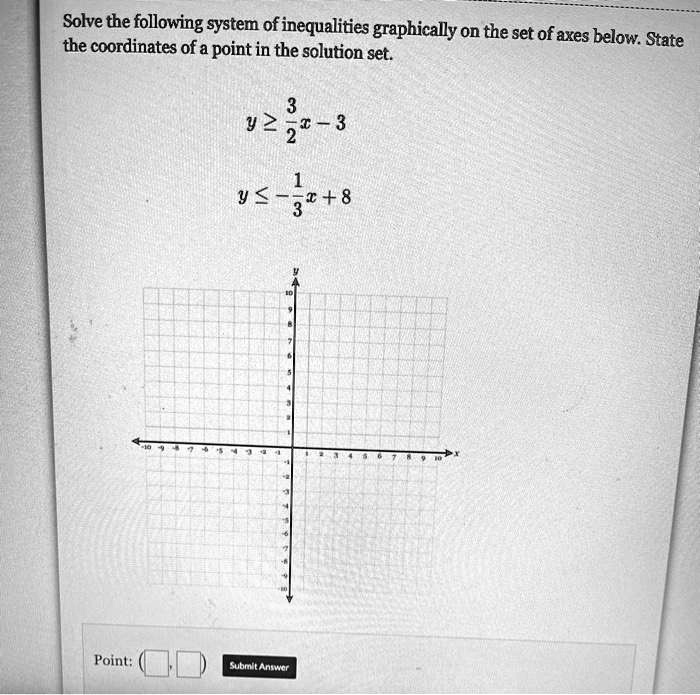 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | 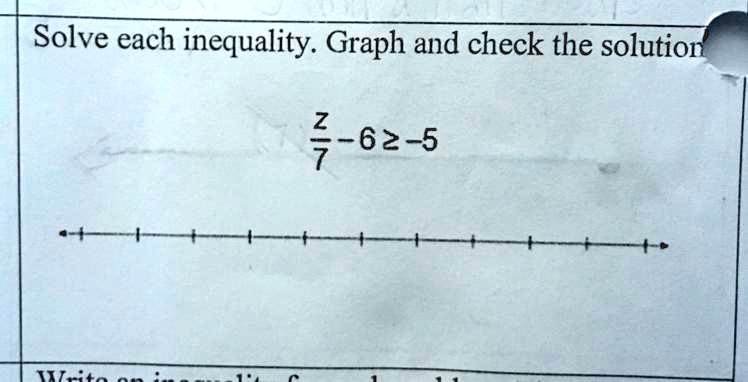 Algebra 1 Mathnmind | 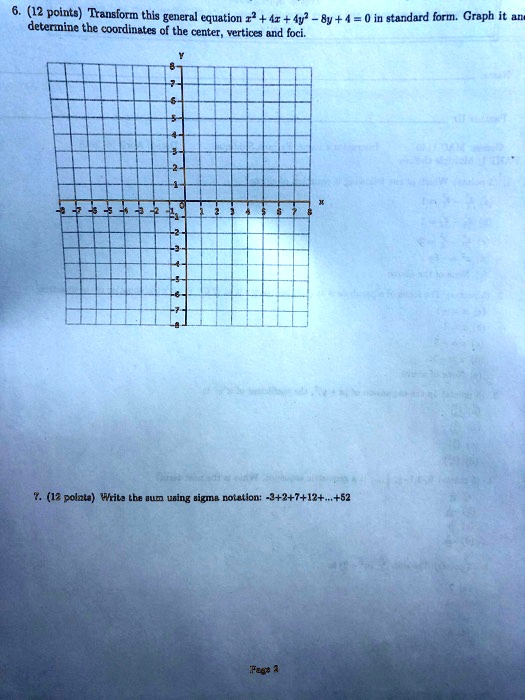 Algebra 1 Mathnmind |
Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind | Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | 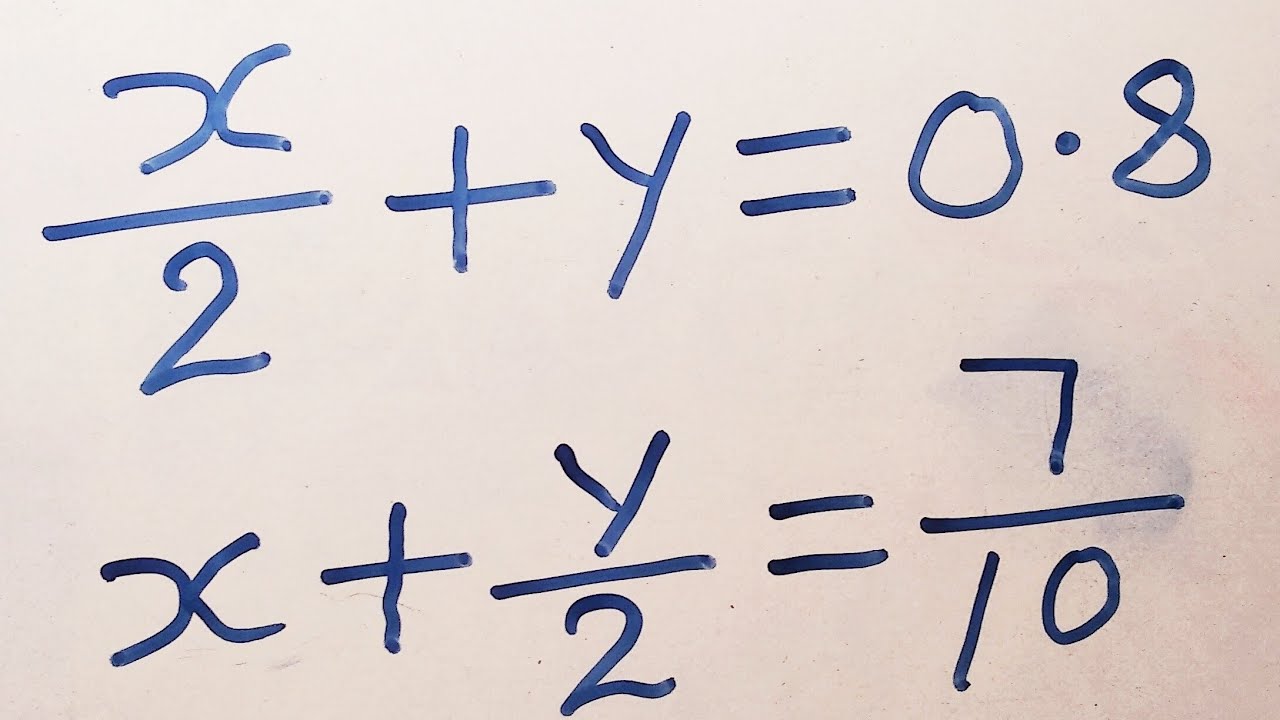 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | 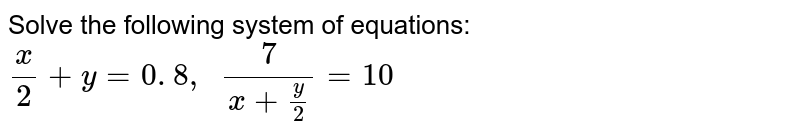 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind | Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | 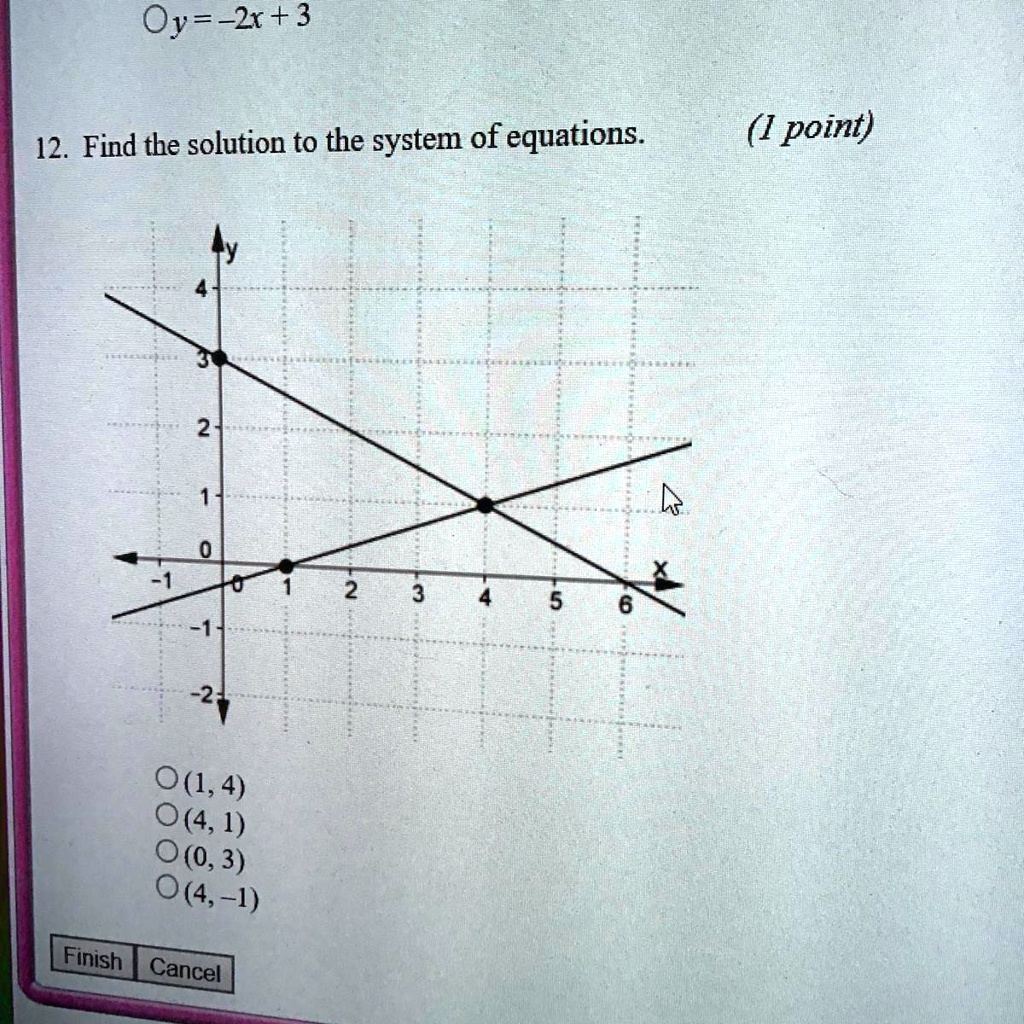 Algebra 1 Mathnmind | 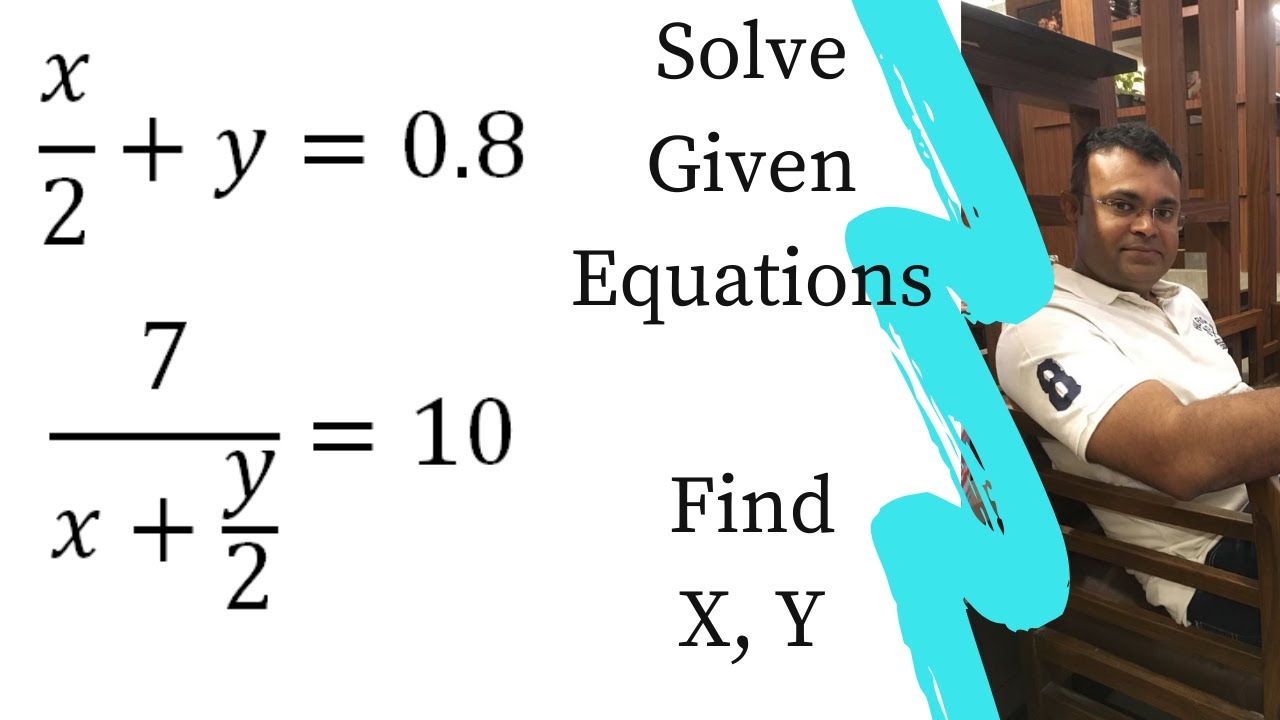 Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind | Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind | Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |  Algebra 1 Mathnmind |  Algebra 1 Mathnmind |
 Algebra 1 Mathnmind |
Web Solve the following system of equations x 2 x 2 y = 08;WebSolve the following systems of equations 2xy=08 x 2y7 =10 Easy Solution Verified by Toppr Equation (1) x2y=16 Equation (2) 7=10x5y Multiply equation (1) by 10 ;
Incoming Term: substitution method calculator mathway, solve equation using substitution method, solve by substitution method calculator, solve by the substitution method, solve equation with substitution method, equation substitution method calculator, solve equations using substitution method, solve using the substitution method, solve the equation by using substitution, the substitution method algebra, algebra 2 substitution method, the substitution method math,



